[지금 무료] 개발자를 위한 컴퓨터공학 1: 혼자 공부하는 컴퓨터구조 + 운영체제 강의 - 인프런
베스트셀러 『혼자 공부하는 컴퓨터 구조 + 운영체제』 저자 무료 직강. 개발자들이 꼭 알아야 할 컴퓨터 구조, 운영체제 전공서 요약집., 개발자 필수지식 컴퓨터 구조와 운영체제강의 하나로
www.inflearn.com
< 인프런의 '개발자를 위한 컴퓨터 공학 : 혼자 공부하는 컴퓨터 구조 + 운영체제' 를 학습하며 정리합니다. >
● 먼저, 컴퓨터는 0과 1로만 이해할 수 있다. 그렇다면, 컴퓨터는 어떻게 3+4가 7이라는 내용을 처리할 수 있는 것일까?
이를 알아보자.
정보 단위
(1) 비트(bit) : 0과 1을 표현하는 가장 작은 정보 단위이다. 따라서 1비트로는 두 가지 정보를 표현할 수 있다.
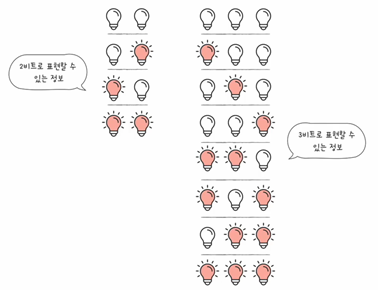
따라서 2비트면 4가지의 정보, 3비트면 8가지의 정보 표현을 할 수 있다.
이를 일반화하여 표현하면, ' n비트로 2^n가지의 정보 표현이 가능하다. '로 정리된다.
프로그램은 결국 수많은 비트, 즉 0과 1로 이루어져 있는 것이다.
다만, 평소에는 더 큰 단위를 사용하여 파일 및 프로그램의 크기를 표현한다.( ex, 바이트, 킬로바이트, 메가바이트, 기가바이트, 테라바이트 .... )

(2) 워드(word) : CPU가 한 번에 처리할 수 있는 정보의 크기 단위
만약, CPU가 한번에 32비트의 정보를 처리할 수 있다면, 이 CPU의 1워드는 32비트이다. 그리고 CPU가 한번에 64비트의 정보를 처리할 수 있다면 1워드가 64비트이다.
이와 관련된 용어는 아래와 같다.
- 하드 워드(half word) : 워드의 절반 크기
- 풀 워드(full word) : 워드 크기
- 더블 워드(double word) : 워드의 두 배 크기
이진법 : 0과 1로 숫자 표현하기
(1) 이진법(bainary)
- 0과 1로 수를 표현하는 방법
- 숫자가 1을 넘어가는 시점에 자리올림
- 우리가 일상적으로 사용하는 진법은 숫자가 9를 넘어갈 때 자리올림하는 십진법(decimal)

따라서 컴퓨터에게 우리가 일상적으로 사용하는 숫자를 알려주려면, 이진수로 알려주면 된다.

여기서 10+1000이라는 이진수로 표현하였을 경우, 이것이 이진법으로 표현한 10, 1000인지 아니면 십진법에 의한 10, 1000인지 구분하기 어렵다. 따라서 아래와 같은 방식으로 표현된다.

(2) 음수 표현하기
컴퓨터는 기본적으로 마이너스(-) 부호를 인식하지 않기 때문에 이를 0,1로 표현이 필요하다.
이에 현대 컴퓨터 사용에 있어 가장 대표적으로 채택된 방식이 ' 2의 보수 ' 방법이다.
이는 ' 어떤 수를 그보다 큰 2^n에서 뺀 값 ' 이다.

정의에 의하여 만약 11(이진법)이라는 수를 음수로 표현하고 싶다면 11(이진법)보다 큰 2^n에서 11(이진법)을 뺴면 된다.
이를 좀 더 쉽게 구하는 방법이 있는데, ' 모든 0과 1을 뒤집고 1 더한 값 '이다.


그런데, 이 방법에서 이런 의문이 생길 수 있다.

- 플래그(flag) 레지스터가 CPU에 존재하는데, 이는 숫자가 '양수 or 음수'라는 표식을 들고 다니는 것으로 헷갈리지 않는다.

(3) 십육진법
이진법으로 숫자를 표시하면 길이가 너무 길어진다는 단점이 있다. ( ex, 32 == 100000 )
그래서 컴퓨터의 데이터를 표현할 때 십육진법도 많이 사용한다.
- 수가 15를 넘어가는 시점에 자리올림

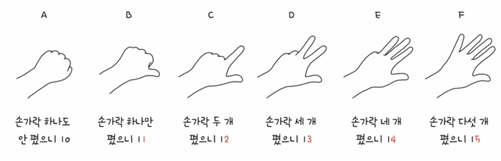
여기서도 10이라는 숫자가 16진법에 의해 16의 의미와 10진법에 의한 16 그대로의 의미인지 파악하기 어려워 이진법과 마찬가지로 아래와 같은 표기법을 가진다.

그런데 10진수를 두고 어째서 16진수를 사용할까??
- 2진수와 16진수 간의 변환이 쉽기 때문이다.

16진수의 각 자리를 2진수로 4칸씩 표현하여 붙이면 2진수로 변환

주어진 2진수를 4칸씩 16진수로 표현하고 붙이면 16진수로 변환
'컴퓨터구조,운영체제' 카테고리의 다른 글
| 02-2) [데이터] 0과 1로 문자를 표현하는 방법 (0) | 2024.01.19 |
|---|---|
| 01) 컴퓨터 구조의 큰 그림 (0) | 2024.01.15 |


댓글